Review Article - (2018) Volume 8, Issue 5
Method Effects Associated with Reversed Items in the 29 Items Spanish Version of RyffûôûôûôûôûôûÂôôûôûôÂûôûôûôûÂôôûôûÂôôûôûÂôô˜ûôûôûôûÂôôûôûÂôôûôûÂôôÂs Well-Being Scales
- Corresponding Author:
- Begoña Espejo
Associate Professor, Departamento de las Ciencias del Comportamiento, Universitat de València. Avenida Blasco Ibáñez, 21, 46010, Valencia; Spain
Tel: +34 963864503
Abstract
Aim
Although they have been frequently used in the literature, there has been much confusion concerning Ryff’s Well-being Scales, such as their factor structure and the effects of method due to the use of reversed items. A common practice nowadays is the use of positively worded items and reversed forms, in order to reduce response bias. However, in many different studies have been seen that this practice introduce method effects in the scores, leading to problems of reliability and validity. This work had two goals: first, to verify the factor structure of the 29-item Spanish version of the original Ryff’s Well-being Scale in an athlete population, and second, to determine whether the method factor associated with the reversed items shown in previous works appears too in a specific sample like athletes. If that happened, the use of this scale would be questionable.
Methods
For this purpose, a sample of 402 competition athletes, both professional and nonprofessional, was used. All the confirmatory factor models found in the literature were tested, using confirmatory factor analysis estimated by means of maximum likelihood with robust corrections.
Results
The best fits were the substantive models of 5 and 6 factors with one factor associated with negative worded items. The results suggest the unsuitability of the 29-item version, suggesting the use of the 54-item scale and avoiding the use of the reversed items to prevent the effect of method.
Conclusions
If this scale is used to measure well-being, we will obtain a measure without validity because, in addition to well-being, we would be introducing into the scores something else that comes from the method effect introduced by the use of reversed items. The use of this scale is not recommended to obtain measures of psychological well-being.
Keywords
Ryff’s Scales, Method Effects, Psychological Well-Being, Confirmatory Factor Analysis, Negative Worded Items, Reversed Items, Validity
Introduction
The study of happiness and its different explanations first emerged in ancient Greece, where Epicurus defined it as a sum of pleasurable moments, laying the groundwork for what we currently consider hedonic well-being [1], whereas Aristotle proposed the need for human beings to live according to an ideal that gives meaning to life, a maxim underpinning the conception of eudaimonic well-being [2]. These ancient roots lead to two orientations: on the one hand, the authors who use the term “Subjective well-being” (SWB) [3-5] and on the other, those who defend that “Psychological well-being” (PWB) is the term that best explains the concept under study [6,7].
Ryff’s proposal, influenced by personal growth models [8-11], theories of the development of a useful life [12,13] and positive mental health guidelines [14], is a multidimensional model that seeks to represent the characteristics of people with high PWB. In this way, individuals with high levels of PWB: (a) feel good about themselves and are aware of their limitations (Self-acceptance - SA), (b) maintain close and satisfactory relationships with others (Positive relations with others-PR), (c) manage their environment to suit their needs (Environmental Mastery - EM), (d) experience a feeling of freedom and individuality (Autonomy - A), (e) have sought and found a goal that combines their goals in life (Life purpose - LP), and (f) carry on a dynamic learning process and continuously develop their skills (Personal Growth - PG). Each of these dimensions of PWB poses a different challenge to people in their attempt to seek happiness and optimum performance [15].
Ryff’s scales were presented for the first time in the year 1989. As of that time, and as a result of the impact of the term PWB, the scales have been subject to validation, adaptation, and modifications both in their length and structure. The debate is still ongoing, and in the past decade, there have been articles by those who are in favor of maintaining the original factor structure of the 6-factor scale [16] and those who advocate that the PWB dimensions share too many characteristics and explanatory power to be considered different dimensions [17-19]. But the debate goes beyond the high correlation between the proposed dimensions, because the different confirmatory studies of factor structure have presented effects of method and correlations among errors in some cases [20], revealing the difficulties posed by the use of reversed items. The scales of Ryff have been constructed with many reversed items, and many of the papers that study the factorial structure, have also studied the effect of method that these items introduce. The use of positively worded items and reversed forms has been recommended traditionally to reduce response bias, and is a commonly used practice nowadays. Nevertheless, empirical studies of the usefulness and adequacy of this practice have been carried out.
An empirical study [21] analyzed the psychometric implications of the use of positive and reversed items in a self-efficacy instrument. A repeated measures design was used, evaluating the participants with positive, reversed, and combined forms of a self-efficacy test. Results showed that, when positive and reversed items are used in the same test, the reliability is flawed and the dimensionality is jeopardized by secondary sources of variance. Furthermore, the variance of the scores is reduced, and the means differ significantly from those in tests in which all items are either positive or reversed, but not combined. These findings show that the use of positive and reversed items in a same test is questionable and no recommended.
On the other hand, the studies concerning the structure of the Ryff’s scale, both in its Anglo- Saxon adaptations and Spanish validations, are presented in Table 1. As can be seen, all the papers that study the factorial structure of the different versions of Ryff’s scales have shown problems. Although the studies with the longer versions of the Ryff scale show acceptable reliability indices, the 14 items per factor version do not show an adequate factor structure. For this reason, it is necessary to study the factor structure of the different versions of the Ryff scales. As the longer version of the Ryff scales (14 items per factor) has not shown good factorial structure and is also too long for its application, shorter versions of this scale have been tested. As can be seen in Table 1, the models in which a method factor associated with the reversed items have been introduced (both for the longer version and for the shorter versions), have always shown better fit.
| References | Items | Sample | Tested models | Best fitting results |
|---|---|---|---|---|
| 6 | 120 | 321 Adults |
6 factors | 6 factors High correlation between factors SA, EM, LP, and PG |
| 44 | 18 | 1108 Adults |
1Factor, 6Factor, 6Factor & 2nd-order | 6 factors High correlation between factors EM and SA |
| 45 | 18 | 4960 Older people |
1Factor, 6Factor | Poor fit 6 factors + 4 correlated errors |
| 19 | 120 | 277 University students |
EFA, 6Factor | 15 factors Analysis with SWLS and MUNSH* 3 factors: 1 = SA, EM, LP and PG; 2 = SWLS and MUNSH; 3 = PR and A. |
| 22 | 84 54 18* |
230 students 420 adults |
1Factor, 2Factors (positive and negative items), 5Factors, 6Factors, 6Factor & 2nd-order | 6 factors + 2nd-order with acceptable fit only in the 18-item scale |
| 18 | 42 12 18 18 |
6282 6038 2731 9240 |
1Factor, 6Factor, 6Factor & 2nd-order, 6factors & method factor | Poor fit Method effects in reversed items High correlation between factors SA, EM, LP |
| 20 | 42 | 1179 Women aged 52 |
1Factor, 6Factor & 2nd-order, 6factors & method factor | 2 method factors + and -, 2 factors PR and A & 2nd-order factor combining the 4 correlated factors SA, EM, LP, and PG |
| 23 | 39 | 467 adults | 1Factor, 2Factors (positive and negative items), 5Factors, 5Factor & 2nd-order, 6Factors, 6Factor & 2nd-order. | The structure proposed by Van Dierendonck did not fit, and 10 items were eliminated New 29-item version, and the best fit 6 dimensions and 1 second-order factor |
| 25 | 54 | 422 people over 65 years | 1Factor, 6Factor, 6Factor & 2nd-order 6 factors & 2 factor of 2nd-order 6 factors & 3 factors of 2nd-order |
Best fit, although poor: 6 factors 6 factors + 2 2nd-order factors: one factor made up of LP and PG (eudaimonic); and the other of PR, A, SA, and EM (hedonistic). |
| 26 | 54 | 169 people over 65 years | 1Factor, 2Factor (PWB & SWB), 5Factor, 5Factor & 2nd-order, 6Factors, 6Factor & 2nd-order, 6F & 2 factor of 2nd order (PWB + SWB) 6Factors & 2nd order combining SA, EM, LP and PG |
There is virtually no difference between the fit of 5 factors, 6 factors, and 6 factors + 2 2nd-order factors (PWB and SWB) It is concluded to continue using the original structure to facilitate replication |
| 46 | 84 54 |
401 students 679 adults |
1Factors, 6Factors 2 factors PR and SA + 2nd order combining the 4 correlated simple factors = SA, EM, LP and PG and with method effects and correlations between errors |
The models that consider the correlation between errors 6 factors + errors |
| 24 | 39 | 919: 592 Spaniards and 327 Colombians | 1Factor, 2Factors (positive and negative items) 3 factors: PR, A and one factor combining SA, EM, LP and PG The former & 2nd order PWB 6Factors, 6Factors & 2nd order combining SA, EM, LP, and PG 6F& 2nd order PWB |
6 factors + 1 second-order PWB High correlations in LP with SA and EM |
| 15 | 42 | 1178 Women aged 52 |
Accuracy studies | The 2nd-order factor combining SA, EM, LP and P is more accurate |
| 28 | 29 | 419 people | 3 factors: PR, A and one factor combining SA, EM, LP and PG The former & RI & V 6Factors, 6Factors & RI & V |
Better fit in the model of 6 factors + Inner Resources +Vitality Authors propose adding these dimensions |
| 27 | 18 29 39 54 |
556 people over 65 years | 1Factor, 2Factor (PWB & SWB), 5Factor, 6Factor, 6factors & method factor. | A method factor (reversed items) is applied to the 6-factor model, improving the fit. Confirms results of Springer & Hauser (2006) in Spain. |
| 31 | 29 | 556 people over 65 years | 6Factor, 1Factor reversed method, 1Factor negative method, 6factors & 2 method factors. | The reversed items provide method error. The structure is still unclear. |
| 48 | 29 | 1646-Chileans | 5Factor, 6Factors, 6Factor & 2nd-order | 6 factors Temporal stability, except for PR |
Table 1: Review of the studies on the factor structure of Ryff’s Psychological Well-Being Scale
In 2004, van Dierendonck [22] examined the factorial and content validity of Ryff’s Scales of Subjective Psychological Well-being (SPWB) in two Dutch samples (psychology students and professionals from a diverse occupational background). The psychometric quality of the SPWB was tested for the versions with 3-items, 9-items and 14-items per scale versions. Even though the factorial validity was only acceptable for the 3-items per scale version, the internal consistency of these scales was too low. So, it was suggested to reduce the length of the 14-item scales to 6 or 8 items, depending on the specific subscale, improving overall psychometric quality and leading to a 39-item version.
In the Spanish linguistic area, this 39-item final version was back-translated and adapted to study the psychometric properties and factorial validity in a Spanish sample of adults [23]. The scale did not present a good fit, so the authors eliminated 10 items and presented the Spanish version with 29 items and 6 dimensions, plus one secondorder factor called PWB. Nevertheless, in a study carried out later [24], the same 39-item version was used to test the six factor model in Spanish and in Colombian populations, showing good fit. In other work, the factor structure of the 54- item version was tested in a sample of adults over 65 years old [25] obtaining poor fits, although the best models were the 6-factor model and the model with 6 factors and 2 second-order factors: one factor that unites Life Purpose and Personal Growth, which, according to the authors, represents eudaimonic well-being, and a second factor that groups Positive Relations with others, Autonomy, Self-acceptance, and Environmental Mastery, and which constitutes hedonistic well-being. In other studies, different versions of the Ryff’s scales have been studied. The 54- item scale was applied to a sample of older Spanish adults [26]. Due to the small sample size (only 165) the analyzes were carried out by grouping items, since the corrections of nonnormality require a higher ratio of subjects per parameter to be estimated. Results showed the best fits for the 6- and 5-factor models with Environmental Mastery and Self-acceptance combined. In other study, the method factor was tested in 4 versions of the scale (19, 29, 39, and 54 items) [27], confirming previous results [17], and reporting the presence of 6 factors and 1 method factor associated with the reversed items.
In order to overcome the criticism of the lack of multicultural adaptation, two new dimensions were added to the PWB scale [28]. For this purpose, the authors used the Inner Resources Scale [29] and the Subjective Vitality Scale [30], and the data showed that the model with the best fit in their sample was the 8-factor model, which presented the original 6 factors and 2 new dimensions: Vitality and Inner Resources. Finally, it was proposed a study of the method effect [31] using data from the 29-item scale of Ryff [23]. This study concluded that the method effect refers to reversed items and not to items with negative particles (no, never), confirming the inadequacy of using reversed items to avoid acquiescence.
The use of the scales of 6 in athlete population is limited to a work that used PWB scales used to investigate the influence of a psychological training program on athletes’ well-being [32,33]. In a Spanish-speaking context, these scales have been used to measure PWB in athletes [34,35] but the structure and reliability in competitive sports population have not been confirmed in any of the scales.
Taking into account the models tested in the English and Spanish versions, the goal of this work is to explore the factor structure of the 29-item version of the Ryff’s Well-being Scales in athlete population by testing all different factorial models, including the study of method factors associated with reversed items [23].
Methods
▪ Participants
The sample was made up of 402 competition athletes, both professional and non-professional, with a mean age of 24.86 years (SD=8.8). The distribution by sex showed a majority of men (75.1%) compared to women (24.9%). The sports practiced by the participants were: basketball (31%), soccer (25.6%), triathlon (22.4%), athletics (5.9%), handball (5.4%), indoor soccer (3.4%), karate (3%), sailing (2.7%), and rhythmic gymnastics (0.5%).
▪ Instruments
Ryff’s Psychological Well-being Scale reduced version, previously translated and adapted into Spanish 23. The instrument has a total of six subscales and 29 items that participants rate on a 6-point Likert-type response format, ranging from 1 (strongly disagree) to 6 (strongly agree). The six scales are Self-Acceptance, Positive Relationships, Autonomy, Environmental Mastery, Life Purpose, and Personal Growth, and the internal consistency rates obtained by the authors ranged between α=0.84 and α =0.70. In addition, the model that obtains a better fit in this Spanish adaptation presents a PWB secondorder factor.
▪ Procedure
After obtaining the athletes’ collaboration and acceptance to participate in the investigation, the scale was administered after a sporting competition by trained personnel. Instructions to the participants indicated that their participation was voluntary, that the questionnaire should be completed individually, and that, at all times, their data would remain confidential and anonymous.
▪ Data analysis
The different confirmatory factor analyses were performed using the statistical package EQS 6.2 for Windows [36]. Since the variables are ordinal, the polychoric correlations matrix has been used, and the statistics have been estimated using maximum likelihood with Satorra-Bentler robust corrections, as recommended [37]. The comparative fit index (CFI), root mean square error of approximation (RMSEA), and chisquare test, together with its degrees of freedom, were used to test the fit of the confirmatory models [38-42]. To assess the method effects associated with reversed items, we introduced an additional factor that is associated with these items, as recommended by different researchers [17,27,43].
The models finally tested are: (1) a onedimensional model [44,45] (2) a two-factor model: PWB made up of the original LP and PG factors and SWB, made up of the PR, A, SA, and EM factors [26,27] (3) a three-factor model: one factor made up of the highly correlated factors SA-EM-LP-PG, and the correlated PR and A factors [46] (4) a five-factor model, combining the EM and SA factors [26] (5) a five-factor model, combining factors EM and SA, with one second-order factor representing PWB [26] (6) the original 6-factor model of Ryff [6] (7) six factors and one second-order factor representing the four theoretically correlated factors SA, EM, LP, and PG [26]; (8) six factors and one second-order factor representing PWB [23]; (9) six factors and two second-order factors, PWB (LP and PG) and SWB (PR, A, SA, and EM); (10) the previous model but with five first-order factors; (11) five factors and a method factor associated with the reversed items [27]; (12) six factors and a method factor 27.
Results
The results (Table 2) show that the models with the best fit are those that control the method effects of the reversed items, with the 5- and 6-factor models (Models 11 and 12) revealing very similar indices. The models with secondorder factors (Models 7, 8, and 9) do not present good fit indices and the errors are higher than .04.
| Model | χ² | df | CFI | RMSEA | |
|---|---|---|---|---|---|
| 1 | 1 factor | 1529.84 | 377 | .938 | .08 |
| 2 | 2 factor: PWB + SWB 26 | 1444.19 | 376 | .943 | .08 |
| 3 | 3 factors: SA-EM-LP-PG, PR, and A 46 | 1290.58 | 374 | .951 | .07 |
| 4 | 5 factors: EM and A combined 26 | 1097.29 | 367 | .961 | .07 |
| 5 | 5 factors + 1 second-order factor (PWB) 26 | 913.26 | 371 | .848 | .06 |
| 6 | 6 factors 6 | 1089.77 | 362 | .961 | .07 |
| 7 | 6 factors + second-order SA-EM-LP-PG 26 | 1243.56 | 373 | .756 | .07 |
| 8 | 6 factors + second-order factor (PWB) 23 | 919.42 | 371 | .846 | .06 |
| 9 | 6 factors + 2 second-order factors (PWB and SWB) 26 | 1325.85 | 371 | .733 | .08 |
| 10 | 5 factors + second-order factor PWB + MET | 606.77 | 335 | .921 | .04 |
| 11 | 5 Factors + MET 27 | 621.86 | 356 | .986 | .04 |
| 12 | 6 factors + MET | 602.48 | 351 | .980 | .04 |
Table 2: Tested models present in the literature
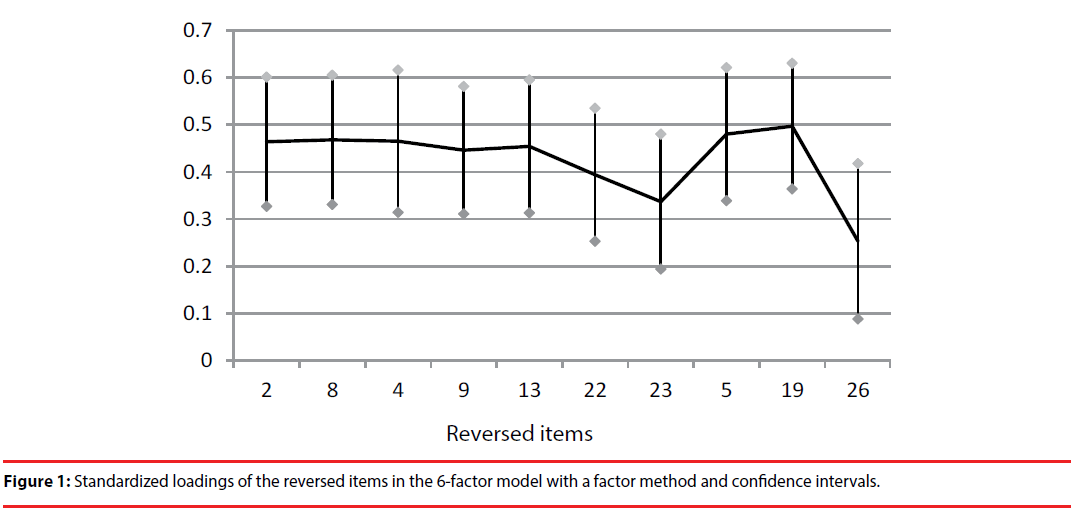
In order to show the amount of method effect, we calculated the mean of this factor associated with the 6-factor model (Model 12) because it is the substantive model most commonly used in the literature, and its goodness-of-fit indices are suitable in this sample. All the loadings of the items included in the method factor were statistically significant, ranging between 0.253 and 0.497. We also calculated the confidence interval of each of these loadings, confirming that the value 0 was not included in any of them (Figure 1), so this factor is real and is important. On the other hand, the t-values ranged between t=8.870 and t=3.674, and all of them were statistically significant.
Discussion
This work had two goals: first, to verify the factor structure of the 29-item Spanish version 23 of the original Ryff’s Well-being Scale 6 in an athlete population, and second, to determine whether the method factor associated with the reversed items shown in previous works [17,27] appears similarly in a specific sample like athletes.
The results confirm the presence of a method factor associated with the reversed items, significantly reducing the error of the substantive 5- and 6-factor models, which presented the best CFI indexes. In addition, we verified that the amount of such method effects is too high to be considered irrelevant.
These results coincide with those obtained by other studies in different versions of the Ryff scales in several languages [17,18,26,27,31], showing that the use of reversed items to avoid acquiescence is inappropriate.
Therefore, it makes no sense to calculate the confirmatory reliability of the factors in the studied version of the scale [47], because several factors include reversed items, and these items include measurement method error in their loadings. Moreover, although the reliability of these factors can be calculated without considering the item variance explained by the method factor, there is no point to this because, in practice, when a questionnaire is used to collect data, the total score is calculated from the observed item scores. In this sense, Cronbach’s alpha would not be an appropriate indicator either, because it is calculated with the observed item score, and this score has been found to contain error derived from the measurement method for reversed items.
Given that reversed items lead to a dead end, the other possibility is to eliminate them of the Spanish version of the scale [23] and only use the non-reversed items to calculate the total score of the factors and their reliability. However, this elimination means that two of the factors (PR and A) only have two indicators. This would lead to a potential problem of content validity and moreover, it might also lead to problems of construct validity of the scale, and discriminant validity among factors. We remind readers that this version was not based on the original 54-item scale, but on a reduced 39-item previous version, finally resulting in a 29-item scale. Therefore, if the number of items is further reduced, all the factors may be lacking content validity.
On the other hand, if a reversed item provides not only specific item variance and random error, but also variance due to measurement method error, then the item is not only measuring PWB but something else besides this construct. In fact, it is not measuring what is intended to measure. This leads to a problem of construct validity. In addition, both in this study and in previous works, carried out with different versions of the Ryff scales, very high correlations between some of the factors were obtained. This could also raise a problem of discriminant validity among factors that should be considered.
Therefore, we consider that this reduced Spanish version of the scale [23] is inappropriate for use with Spanish population. Regarding the original scale, it could be thought that having 54 items could be used instead. However, half of the items of each factor are reversed, and in previous works carried out with this scale, it has been observed that there is a method effect introduced by them. Since using only the non-inverted items would reduce the number of items by half, it is possible that this will lead to a content validity problem. So, the psychometric properties of the original 54 items scale, without the inverted items, must be studied before, in order to determine whether content validity decreases excessively (because the number of items will decrease) and whether there is too much correlation among factors. If correlations are too high, this could lead to a problem of discriminant validity among latent dimensions.
Finally, some limitations of this paper must be considered. On the one hand, the sample size: with a larger sample, other analyses could have been made which would have enabled us to complement the results obtained. In addition, the results need to be analyzed in the context of the specific sample studied, because the measure of PWB in athletes may be mediated by the objective and subjective outcome obtained after the competition. This datum may have partly altered the conclusions reached through the analyses conducted, although, in general, they coincide with those obtained by other authors in different studies.
Author Contributions
Author Irene Checa did the conception and design of the study, acquisition and analysis of data, as well as the drafting of the manuscript and figures. Author Begoña Espejo modified and reorganized the paper.
Informed Consent
Informed consent was obtained from all individual participants included in the study.
References
- McMahon DM. Happiness: A history. New York, USA (2006).
- Vázquez C, Hervás G, Rahona JJ, et al. Psychological well-being and health. Contributions of positive psychology. Ann. Clin. Health. Psych 5(5), 15-27 (2009).
- Diener E. Subjective well-being. Psychol. Bull 95(3), 542-575 (1984).
- Pavot W, Diener E. Review of the satisfaction with life scale. New York, USA. (2009).
- Diener E. Assessing subjective well-being: Progress and opportunities. New York, USA. (2009).
- Ryff CD. Happiness is everything, or is it? explorations on the meaning of psychological well-being. J. Pers. Soc. Psychol 57(6), 1069-1081 (1989).
- Ryff CD. Psychological well-being in adult life. Curr. Direct. Psych. Sci 4(4), 99-104 (1995).
- Allport GW. Traits revisited. Am. Psychol 21(1), 1-10 (1966).
- Jung CG. Modern man in search of a soul. Florence, USA. (1932).
- Maslow AH. Toward a psychology of being. England. (1968).
- Rogers CR. The interpersonal relationship: The core of guidance. Harvard. Edu. Rev 32(4), 416-429 (1962).
- Bühler C. The curve of life as studied in biographies. J. Appl. Psychol 19(4), 405-409 (1935).
- Erikson EH. Identity and the life cycle. England. (1959).
- Jahoda M. Current concepts of positive mental health. New York, USA. (1958).
- Keyes CLM, Shmotkin D, Ryff CD. Optimizing well-being. J. Personal. Soc. Psych 82(6), 1007-1022 (2002).
- Ryff CD, Singer BH. Best news yet on the six-factor model of well-being. Soc. Sci. Res 35(4), 1103-1119 (2006).
- Springer KW, Hauser RM. An assessment of the construct validity of ryff's scales of psychological well-being: Method, mode, and measurement effects. Soc. Sci. Res 35(4), 1080-1102 (2006).
- Springer KW, Hauser RM, Freese J. Bad news indeed for ryff’s six-factor model of well-being. Soc. Sci. Res 35(4), 1120-1131 (2006).
- Kafka GJ, Kozma A. The construct validity of ryff's scales of psychological well-being (SPWB) and their relationship to measures of subjective well-being. Soc. Indicators. Res 57(2), 171-190 (2002).
- Abbott RA, Ploubidis GB, Huppert FA, et al. Psychometric evaluation and predictive validity of ryff's psychological well-being items in a UK birth cohort sample of women. Health. Qual. Life. Outcomes 4(1), 76 (2006).
- Suárez-Álvarez J, Pedrosa I, Lozano LM, et al. Using reversed items in likert scales: A questionable practice. Psicothema 30(2), 149-158 (2018).
- van Dierendonck D. The construct validity of ryff's scales of psychological well-being and its extension with spiritual well-being. Personal. Ind. Diff 36(3), 629-643 (2004).
- Díaz D, Rodríguez-Carvajal R, Blanco A, et al. Adaptación española de las escalas de bienestar psicológico de ryff. Psicothema18(3), 572-577 (2006).
- van Dierendonck D, Díaz D, Rodríguez-Carvajal R, et al. Ryff's six-factor model of psychological well-being, a spanish exploration. Soc. Indicators. Res 87(3), 473-479 (2008).
- Triadó C, Villar F, Solé C, et al. Construct validity of ryff's scale of psychological well-being in spanish older adults. Psych. reports 100(3), 1151 (2007).
- Tomás Miguel JM, Meléndez Moral JC, Navarro Pardo E. Modelos factoriales confirmatorios de las escalas de ryff en una muestra de personas mayores. Psicothema 20(2), 304-310 (2008).
- Tomás JM, Meléndez JC, Oliver A, et al. Efectos de metodo en las escalas de ryff: Un estudio en poblacion de personas mayores. Psicologica 31(2), 383-400 (2010).
- Rodríguez-Carvajal R, Díaz-Méndez D, Moreno-Jiménez B, et al. Vitalidad y recursos internos como componentes del constructo de bienestar psicológico. Psicothema 22(1), 63-70 (2010).
- Howden JW. Development and psychometric characteristics of the spirituality assessment scale, USA. (1993).
- Ryan RM, Frederick C. On energy, personality, and health: Subjective vitality as a dynamic reflection of well-being. J. Pers 65(3), 529-565 (1997).
- Tomás JM, Sancho P, Oliver A, et al. Efectos de método asociados a ítems invertidos vs. ítems en negativo revista mexicana de psicología. Sociedad. Mexicana. De. Psicología 29(1), 105-115 (2012).
- Lundqvist C. Well-being in competitive sports-the feel-good factor? A review of conceptual considerations of well-being. Int. Rev. Sport. Exercise. Psych 4(2), 109-127 (2011).
- Edwards DJ, Steyn BJ. Sport psychological skills training and psychological well-being. South African J. Res. Sport, Phy. Edu. Recreat 30(1), 15-28 (2008).
- Liberal R, Escudero JT, Cantallops J, et al. Impacto psicológico de las lesiones deportivas en relación al bienestar psicológico y la ansiedad asociada a deportes de competición. Revista. De. Psicología. Del. Deporte23(2), 451-456 (2014).
- Romero Carrasco AE, Brustad RJ, Campbell RZ, et al. Bienestar psicológico y psicopatología: Estudio de un caso de intervención en el equipo técnico y deportistas de un club de tenis. Revista. De. Psicología. Del. Deporte22(2), 387-394 (2013).
- Bentler PM, Wu EJC. EQS for windows (version 6.2). (2011).
- Bentler PM. EQS 6 structural equations program manual. Encino, CA: Multivariate Software Inc. (2006)
- Hoyle RH, Panter AT. Writing about structural equation models. In: Hoyle RH, ed. Structural equation modeling: Concepts, issues, and applications. USA, (1995).
- Hu L, Bentler PM. Evaluating model fit. In: Hoyle RH, ed. Structural equation modeling: Concepts, issues, and applications. Thousand Oaks, CA, USA, (1995).
- Hu L, Bentler PM. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Struc. Equat. Model 6(1), 1-55 (1999).
- Kaplan D. Review of structural equation modeling: Foundations and extensions. J. Edu. Measure 39(2), 183-186 (2002).
- Marsh HW, Balla JR, Hau K. An evaluation of incremental fit indices: A clarification of mathematical and empirical properties. In: Advanced structural equation modeling: Issues and techniques. Hillsdale, USA. (1996).
- Tomás JM, Hontangas PM, Oliver A. Linear confirmatory factor models to evaluate multitrait-multimethod matrices: The effects of number of indicators and correlation among methods. Multivariate. Behav. Res 35(4), 469-499 (2000).
- Ryff CD, Keyes CLM. The structure of psychological well-being revisited. J. Pers. Soc. Psychol 69(4), 719-727 (1995).
- Clarke PJ, Marshall VW, Ryff CD, Wheaton B. Measuring psychological well-being in the canadian study of health and aging. Int. Psychogeriatrics 13(S1), 79-90 (2001).
- Burns RA, Machin MA. Investigating the structural validity of ryff’s psychological well-being scales across two samples. Soc. Indicators. Res 93(2), 359-375 (2009).
- Raykov T. Bias of coefficient afor fixed congeneric measures with correlated errors. App. Psych. Measure 25(1), 69-76 (2001).